Formule mathématique du théorème de Pythagore
« Dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. »
A quoi sert le théorème de Pythagore ?
Cette formule sert à calculer la longueur d’un côté d’un triangle rectangle lorsque l’on connait la longueur des deux autres. Par ailleurs, cette formule sert également parfois à démontrer qu’un triangle est ou n’est pas rectangle.
► Demander un Cours Particulier de Math ◄
Comment calculer le théorème de Pythagore ?
Tout d’abord, nous avons besoin de l’hypoténuse. L’hypoténuse est le plus grand côté du triangle mais également le côté opposé à l’angle droit.
Pour calculer simplement la longueur d’un côté d’un triangle rectangle vous devez appliquer cette formule :
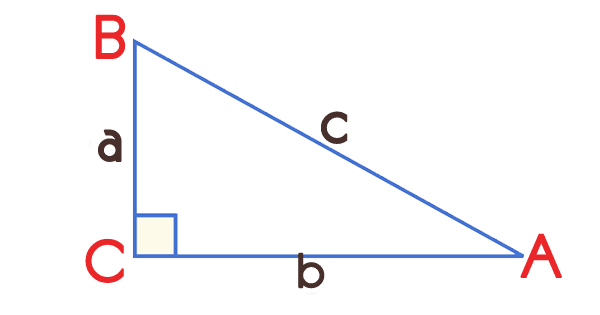
– Dans le triangle rectangle ABC rectangle en A ► BC² = AB² + AC²
– Dans le triangle rectangle ABC rectangle en B ► AC² = AB² + BC²
– Dans le triangle rectangle ABC rectangle en C ► AB² = AC² + BC²
► Obtenir un cour particulier sur Pythagore ◄
Exercice de Math sur Pythagore
Soit RFA un triangle rectangle en F | RF = 3cm et FA = 4cm | Calculer RA.
Dans le triangle RFA rectangle en F, d’après le théorème de Pythagore :
RA² = RF² + FA² donc
RA² = 3² + 4² donc
RA² = 9 + 16 donc
RA² = 25
RA = √25
RA = 5cm
Exercice #2
Dans le triangle PIF rectangle en I | PI = 4cm et PF = 7cm | Calculer IF.
Dans le triangle PIF rectangle en I, d’après le théorème de Pythagore :
IF² = PI² + PF² donc
IF² = 7² + 4² donc
IF² = 49 + 16 = 65
IF = √65
IF = environ 8,06 cm
